How To Find The Median By Looking At A Histogram

Y'all can connect the shape of a histogram with the mean and median of the statistical data that you use to create it. Conversely, the relationship between the hateful and median tin can help yous predict the shape of the histogram.

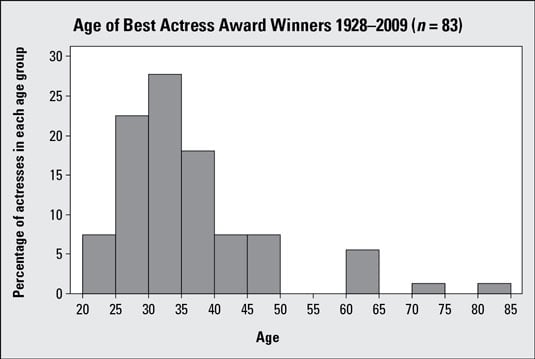
The preceding graph is a histogram showing the ages of winners of the All-time Actress Academy Laurels; y'all can encounter it is skewed right. The following table includes calculations of some basic (that is, descriptive) statistics from the data prepare. Examining these numbers, you discover the median historic period is 33.00 years and the mean age is 35.69 years:

The mean age is higher than the median age because of a few actresses that were quite a fleck older than the rest when they won their awards. For instance, Jessica Tandy won for her role in Driving Miss Daisy when she was 81, and Katharine Hepburn won the Oscar for On Golden Pond when she was 74. The relationship between the median and mean confirms the skewness (to the right) constitute in the first graph.

Hither are some tips for connecting the shape of a histogram with the mean and median:

If the histogram is skewed correct, the mean is greater than the median.

This is the case because skewed-right information have a few large values that drive the mean upward but do non touch where the exact middle of the data is (that is, the median).
If the histogram is close to symmetric, and then the mean and median are close to each other.

Close to symmetric ways the data are roughly the same in superlative and location on either side of the center of the histogram; it doesn't need to be exact.

Close is defined in the context of the information; for instance, the numbers 50 and 55 are said to be close if all the values lie betwixt 0 and 1,000, but they are considered to exist further autonomously if all the values lie betwixt 49 and 56.

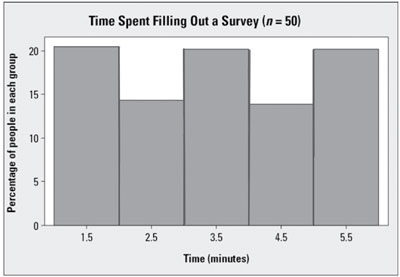
The histogram shown in this graph is close to symmetric. Its hateful and median are both equal to 3.5:
If the histogram is skewed left, the mean is less than the median.

This is the case because skewed-left data have a few small values that drive the mean downward just exercise not bear upon where the exact middle of the data is (that is, the median).

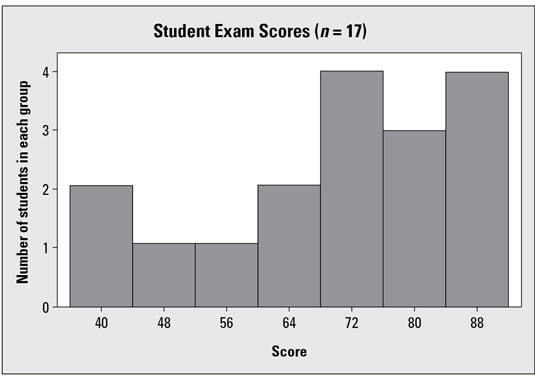
The following graph represents the test scores of 17 students, and the data are skewed left. The mean and median of the original information set are calculated to be 70.41 and 74.00, respectively. The mean is lower than the median due to a few students who scored quite a bit lower than the others. These findings match the general shape of the histogram shown in the graph:

If for some reason you don't have a histogram of the data, and yous only accept the mean and median to go by, you can compare them to each other to become a rough thought every bit to the shape of the data set.

If the mean is much larger than the median, the data are generally skewed right; a few values are larger than the remainder.
If the hateful is much smaller than the median, the data are generally skewed left; a few smaller values bring the mean downwards.
If the mean and median are close, you know the data is fairly balanced, or symmetric, on each side (merely not necessarily bell-shaped).